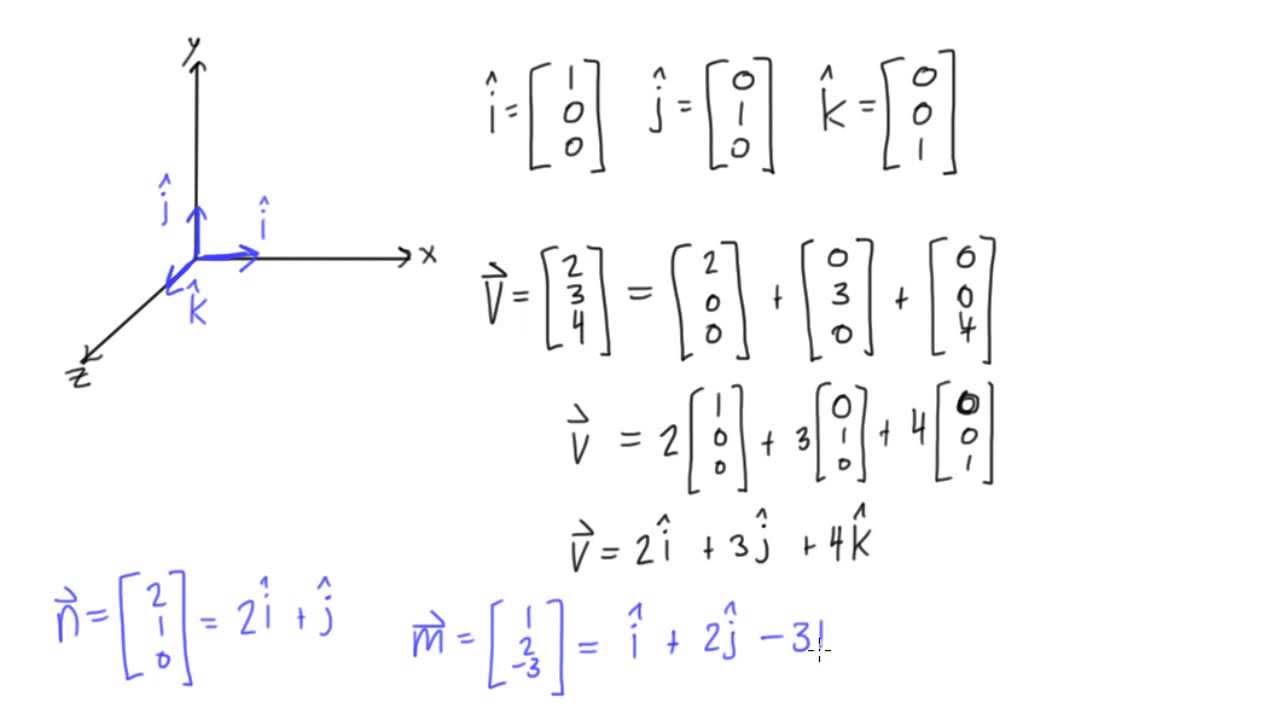I J K Vectors

Then you take the second vector which is b which is minus 2.

I j k vectors. But the way to do it if you re given engineering notation you write the i j k unit vectors the top row. Find p q. Math quad hat i cdot hat i hat j hat k hat i hat i hat j hat k cos theta sqrt 3 cos theta math. And that is probably how you saw them written last year.

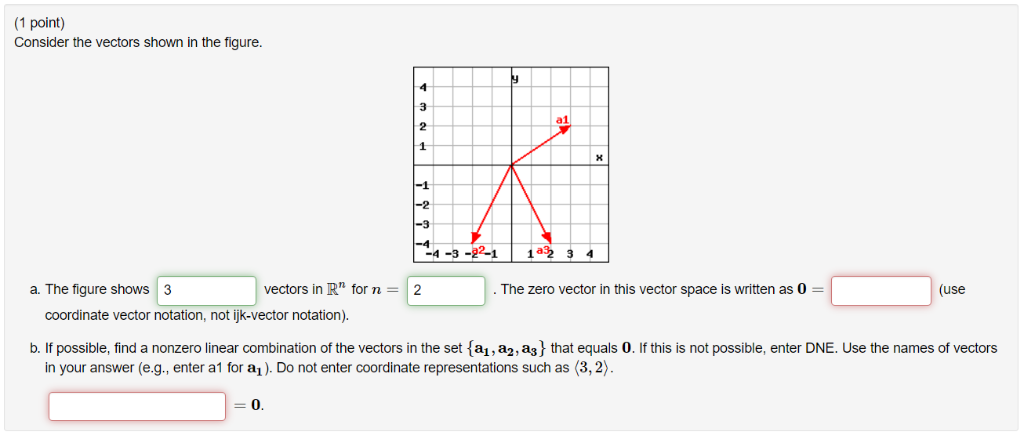
K x k 0 then why i x j k this is because i along x axis and y along y axis thus angle between them will be 90 degree. Adding vectors if two vectors are added together the resultant is found by placing the vectors to be added end to end. Basically it s a more standard way of expressing vectors without any relative angles. As sin 90 1.

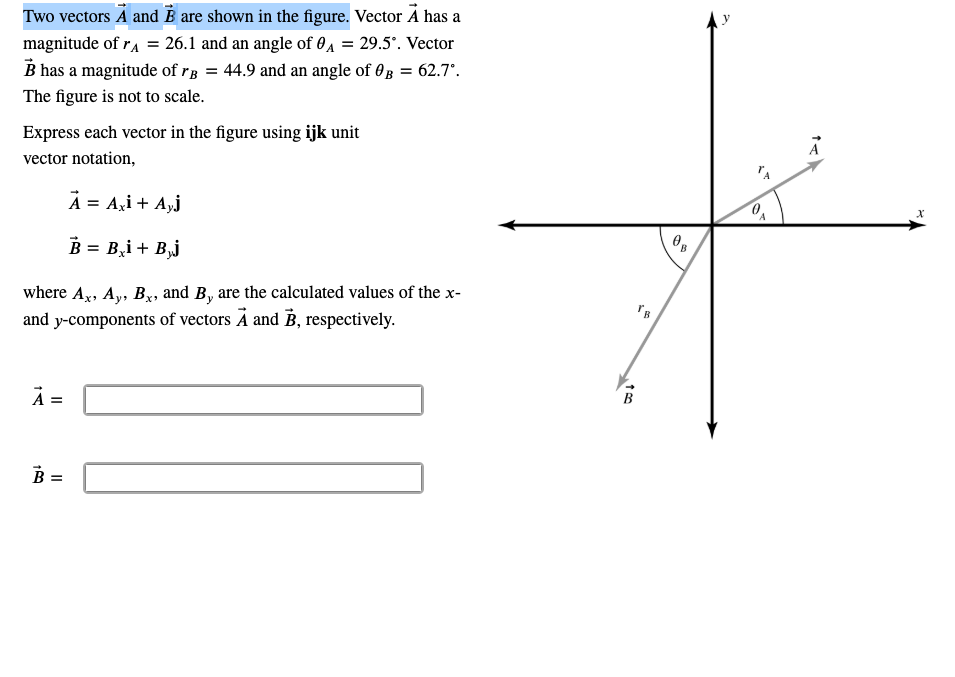
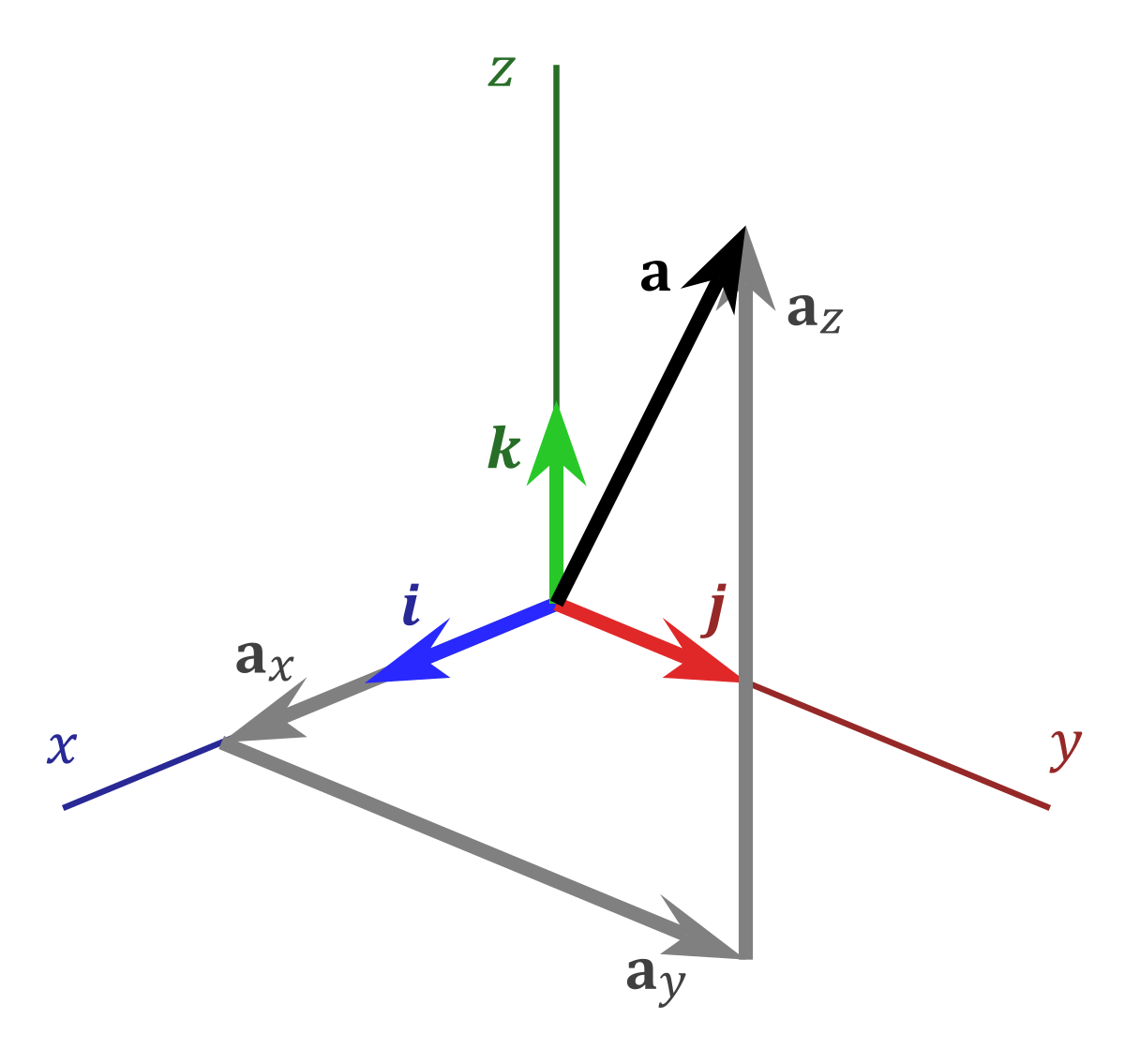
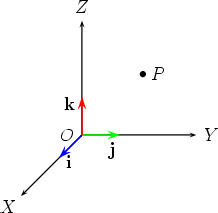
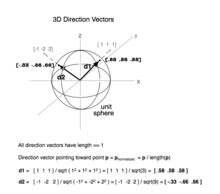
Where i j and k are the unit vector in the x y and z directions respectively and has magnitude of one unit. Example p 3i j q 5i j. Vectors can be broken into i j and k representing the x y and z axes respectively. Where l m and n stands for the respective direction cosines of the vectors.

So it s 5 minus 6 3. You ll usually do dot product calculations with the vectors in component form. Since two identical vectors produce a degenerate parallelogram with no area the cross product of any vector with itself is zero a a 0 applying this corollary to the unit vectors means that the cross product of any unit vector with itself is zero. If the vectors are given in unit vector form you simply add together the i j and k values.

Converting to ijk convert the vector to ijk notation. Converting to ijk in general if you have the m a. I i j j k k. As curl or rotation of two vectors give the direction of third vector therefore i x j 1 sin 90 k i x j k but j x i k because.

It is also observed that two vectors are where. Vectors have magnitude and direction. Since thei j i. Then you write the first vector in the cross product because order matters.

In 2 space since i 1 0 and j 0 1 we get i i 1 j j 1 and i j 0 in 3i j. Unit vectors may be used to represent the axes of a cartesian coordinate system for instance the unit vectors in the direction of the x y and z axes of a three dimensional cartesian coordinate system are they form a set of mutually orthogonal unit vectors typically referred to as a standard basis in linear algebra. For example i can express 50 n at an angle of 30 degrees relative to the horizontal in unit vector notation by finding the x and y components like usual using cos 30 and sin 30 times the magnitude 50.